-
技术专区
-
罗氏线圈变比计算:公式、步骤与实操案例全指南
发布:西安普科科技浏览次数:一、罗氏线圈变比计算的核心意义
罗氏线圈(Rogowski Coil)作为一种空心式电流传感器,凭借响应速度快、测量范围广、无磁饱和等优势,广泛应用于电力系统、工业控制、新能源设备等领域的电流测量。而变比计算是罗氏线圈选型、校准及精准测量的核心环节 —— 它直接决定了二次输出信号与一次被测电流的对应关系,若变比计算偏差,会导致测量数据失真,影响设备控制精度或系统安全运行。因此,掌握罗氏线圈变比计算方法,是电力工程师、设备运维人员的必备技能。
二、罗氏线圈变比的基本原理
罗氏线圈的变比(又称 “匝数比” 或 “变换系数”)本质是一次被测电流与二次感应电压 / 电流的比例关系,其原理基于电磁感应定律:
当一次侧有变化的电流
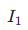 通过时,线圈会感应出与电流变化率
通过时,线圈会感应出与电流变化率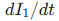 成正比的二次电压
成正比的二次电压 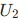 ,再通过积分器将电压信号转换为与一次电流成正比的输出信号,最终实现电流测量。
,再通过积分器将电压信号转换为与一次电流成正比的输出信号,最终实现电流测量。核心逻辑:变比 = 一次电流范围 / 二次输出信号范围,需结合线圈匝数、几何参数及外接电路参数综合计算。

三、罗氏线圈变比计算的核心公式与参数说明
1. 基础变比公式(理想状态)
罗氏线圈的理想变比K,计算公式为:
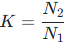
其中:N1= 一次侧匝数(罗氏线圈为空心结构,一次侧通常为 1 匝,即被测导体直接穿过线圈);N2= 二次侧线圈匝数(线圈实际缠绕的总匝数)。
推导说明:理想状态下,忽略线圈电阻、漏感等损耗,根据电磁感应定律,一次磁动势等于二次磁动势(I1×N1=I2×N2),因此电流变比K=I1/I2=N2/N1。
2. 实际应用中的变比公式(含外接电路)
实际测量中,罗氏线圈需搭配积分器使用,此时变比需结合积分器参数修正,完整公式为:
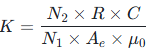
关键参数详解:
N1:一次侧匝数(默认 1 匝,特殊定制线圈需按实际标注取值);
N2:二次侧匝数(线圈出厂时标注,如 1000 匝、2000 匝);
R:积分器反馈电阻(单位:Ω,常见取值 1kΩ-100kΩ);
C:积分器反馈电容(单位:F,常见取值 1nF-100nF);
Ae:线圈有效截面积(单位:m²,由线圈内径、外径及长度计算得出);
μ0:真空磁导率(常量,取值
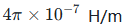 )。
)。3. 电压变比与电流变比的转换
若需将二次电流信号转换为电压信号输出,电压变比KU
计算公式为:
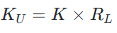
其中
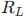 为二次侧负载电阻(单位:Ω),即电压变比 = 电流变比 × 负载电阻。
为二次侧负载电阻(单位:Ω),即电压变比 = 电流变比 × 负载电阻。四、罗氏线圈变比计算的详细步骤(实操案例)
1. 准备参数(以某工业级罗氏线圈为例)

2. 计算理想电流变比
根据基础公式:
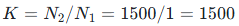 (即一次电流 1500A 时,二次电流 1A)。
(即一次电流 1500A 时,二次电流 1A)。3. 计算实际应用变比(含积分器)
代入完整公式:
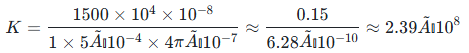
说明:实际变比需结合积分器参数修正,若无需高精度测量,可简化使用理想变比估算。
4. 计算电压变比(假设负载电阻
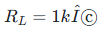 )
)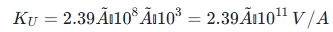
含义:一次电流每变化 1A,二次输出电压变化
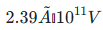 (实际应用中需根据测量范围调整负载电阻)。
(实际应用中需根据测量范围调整负载电阻)。5. 验证与校准
计算完成后,可通过标准电流源进行校准:输入已知一次电流
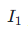 ,测量二次输出信号
,测量二次输出信号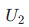 或
或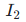 ,验证
,验证 是否与计算变比一致,偏差需控制在 ±1% 以内(高精度场景 ±0.1%)。
是否与计算变比一致,偏差需控制在 ±1% 以内(高精度场景 ±0.1%)。五、罗氏线圈变比计算的注意事项
参数准确性:线圈匝数、有效截面积需以出厂说明书为准,积分器电阻、电容需用万用表实测(避免标称值与实际值偏差);
理想与实际差异:低频测量(<1kHz)时,线圈电阻、漏感影响较小,可使用理想公式;高频测量(>1MHz)需用完整公式,且需考虑寄生参数;
线圈安装影响:被测导体需穿过线圈中心,若偏移中心轴线,会导致有效截面积Ae变化,需重新计算变比;
温度补偿:高温环境下,电阻、电容参数会漂移,需在计算时加入温度补偿系数(如金属膜电阻温度系数 ±50ppm/℃);
特殊场景修正:测量非正弦电流(如谐波电流)时,需结合傅里叶变换,按不同频率分段计算变比。
六、罗氏线圈变比计算的应用场景
电力系统:高压输电线路电流测量,变比需匹配继电保护装置的输入范围(如 1000:1、2000:1);
工业控制:变频器、逆变器的输出电流检测,需根据设备额定电流计算变比,确保二次信号适配 PLC、示波器等设备;
新能源领域:光伏逆变器、储能系统的电流监测,变比需满足高精度(±0.2%)、宽频带(10Hz-1MHz)要求;
科研实验:脉冲电流、瞬时大电流测量,需定制线圈并精准计算变比,适配实验数据采集需求。
七、总结
罗氏线圈变比计算的核心是明确 “匝数比” 与 “外接电路参数” 的关联,理想状态下可简化为匝数比计算,实际应用中需结合积分器、负载电阻等参数修正。掌握变比计算方法,能帮助工程师精准选型、校准罗氏线圈,避免因变比偏差导致的测量误差。无论是电力系统运维、工业设备调试,还是科研实验,精准的变比计算都是罗氏线圈高效应用的前提。
以上内容由普科科技/PRBTEK整理分享, 西安普科电子科技有限公司致力于示波器测试附件配件研发、生产、销售,涵盖产品包含电流探头、差分探头、高压探头、无源探头、罗氏线圈、电流互感器、射频测试线缆及测试附件线等。旨在为用户提供高品质的探头附件,打造探头附件国产化知名品牌。更多信息,欢迎登陆官方网站进行咨询:https://www.prbtek.cn/
2025-11-28相关仪器




